前言
关于语义分割领域的常用评价指标进行一些个人解读,欢迎批评指正。
本来是想连目标检测的一起说了的,但是关于AP的一些东西始终有疑问,留着后面搞懂了再写一篇吧。
前置理解
在解读这些评价指标之前,需要对深度学习方法有一个基础认识。
首先,评价指标,是指测试阶段将预测结果与真实值进行比对得到的量化结论。评价指标(Metric)和损失函数(Loss)有联系也有区别,目前在我个人理解来说,评价指标是以实用的角度评价模型,只关心模型的结果,而损失函数是从数学的角度收敛模型,但损失往往应该与一个你最关心的评价指标相对应,通过收敛损失能够达到向指标增大的方向靠拢。并且,损失应该是容易优化的,很多时候它们对模型参数可微,甚至是凸的。下面引[10]中的例子做说明。
假设某同学备战高考,他给自己定下了一个奋斗的方向,即每周要把自己的各科总成绩提高5分;经过多年的准备,终于在高考中取得了好成绩(710分,总分750),被北大录取。
分析该例子,该同学“每周要把自己的各科总成绩提高5分”这个指导原则相当于目标函数,在这个指导原则的指引下,想必该同学的总分会越来越高,即模型被训练的越来越好。
最终,该同学高考成绩优异,相当于模型的测试效果良好,至于用从哪个角度评价这名同学,可以用其高考总分与750分的差距来衡量,也可以用其被录取的大学的水平来衡量,这就如同模型的评估指标是多种多样的,比如分类问题中的准确率、召回率等。
当然,模型的评估指标多样,模型的损失函数也是多样的;该例中,该同学可以将“每周要把自己的各科总成绩提高5分”作为指导原则,也可将“每周比之前多学2个知识点”作为指导原则。
另外,如果该同学将“每周模拟高考总分与750分的差距”同时作为指导原则与评价角度,则类似于线性回归模型将“MSE均方误差”同时作为损失函数与评估指标。
该例中,备考的“指导原则”相当于“损失函数”,“评价角度”相当于“评估指标”,该同学相当于一个机器学习模型。
其次,在多分类任务中,通常包含$n$个类别,而对于某一样本的最终预测只能是$n$个类别中的一个。但是,算法对一个样本的类别预测通常以置信度的形式表示,最终选择置信度最高的类别作为预测输出。
最后,多分类任务对于每个类来看,可以看作是一个二分类问题,以样本对于该类别预测是否正确作为区分。
混淆矩阵(Confusion Matrix)
混淆矩阵用于直观的显示模型预测结果的情形。 混淆矩阵中的横纵轴都是类别,对于$p_{ij}$(横坐标为$i$,纵坐标为$j$处的值),其含义为属于类别$i$并被预测为类别$j$的样本数量(在语义分割中通常样本等同于像素)。也就是说,每个位置的横坐标表示模型的预测,纵坐标表示真实标签。
对于二分类问题,混淆矩阵可以表示如下:
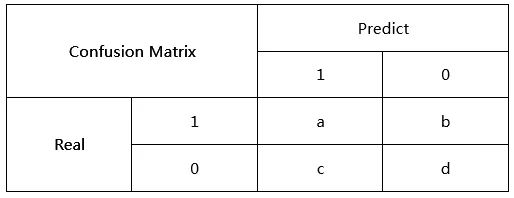
若令其中$1$表示正类,$0$表示负类,则可以定义如下四个量:
- TP(True Positive):将正样本预测为正类的数量,即图中的$a$。
- FN(False Negative):将正样本预测为负类的数量,即图中的$b$。
- FP(False Positive):将负样本预测为正类的数量,即图中的$c$。
- TN(True Negative):将负样本预测为负类的数量,即图中的$d$。
对于多分类问题,只是把该矩阵由$2 \times 2$变化为$n \times n$,其中$n$表示类别数量。
从混淆矩阵中我们可以获得一些基础信息,如:
- $i$行的和$\sum^n_{j=1}p_{ij}$表示数据集中属于类别$i$的样本个数
- $j$列的和$\sum^n_{i=1}p_{ij}$表示模型预测中属于类别$j$的样本个数
- 矩阵中所有元素的和$\sum^n_{i=1}\sum^n_{j=1}p_{ij}$表示图像中的总样本个数
- …
精确率(Precision)和召回率(Recall)
这两个指标都是针对某一类别而言的,是分类任务的常用评价指标。
精确率又称查准率,含义是对于模型预测中属于类别$j$的样本,预测结果正确的比例。例如对于二分类问题,正类的精确率$Precision_{positive} = \frac{TP}{TP+FP} = \frac{a}{a+c}$。
召回率又称查全率,如果说精准率是站在预测的角度看问题,那么召回率就是站在现实的角度看问题,其含义是对于数据集中属于类别$i$的样本,被正确预测的比例。例如对于二分类问题,负类的召回率$Recall_{negative} = \frac{TN}{FP+TN} = \frac{d}{c+d}$。
准确率(Accuracy)
准确率需要和精确率区别开,准确率是站在预测的整体角度看问题,其含义是预测正确的样本占所有样本的比例。例如对于二分类问题,预测的准确率$Accuracy_{predict} = \frac{TP+TN}{TP+FN+FP+TN} = \frac{a+d}{a+b+c+d}$。可以看出,准确率其实就是混淆矩阵对角线元素和与所有元素和的比值。
F1指标(F1 Score)和F-Beta指标(F-Beta Score)
单独用精确率或召回率有时不能很好的评估模型,例如在二分类问题中,模型选择对所有样本预测为正类,此时所有正类样本都被“准确”的预测了,正类召回率为$1$,但模型实际上很差。
F1指标就是用来平衡精确率和召回率的重要程度的度量指标,它被定义为两者的调和平均值,表示二者重要程度一致。F1指标的计算公式如下:
调和平均值的一个重要特性就是如果两者极度不平衡,调和平均值会很小,只有当两者都较高时,调和平均才会比较高。
而F-Beta指标则是更一般的形式,他的计算方式如下:
其中参数$\beta$决定了精确率和召回率的重要程度比值,当$\beta>1$时召回率比重更大,当$\beta<1$时精确率比重更大。
特异性(Specificity)和敏感性(Sensitivity)
关于这两个指标,似乎是仅针对于二分类问题而言的,这里只谈一些个人理解。
还是参照二分类的混淆矩阵,特异性实际上指的就是负类的召回率$Recall_{negative}$,而敏感性则指的是正类的召回率$Recall_{positive}$,看了网上许多解释,都是聚焦在医疗领域,把患病作为正类,健康作为负类,说什么敏感性越高,漏诊概率越低;特异性越高,确诊概率越高。
个人理解,实际上就是召回率在特定情况下的应用吧。
交并比(Intersection over Union,IoU)和平均交并比(mIoU)
给定两个区域$A$和$B$,IoU就是两区域的交集与两区域并集的比值:
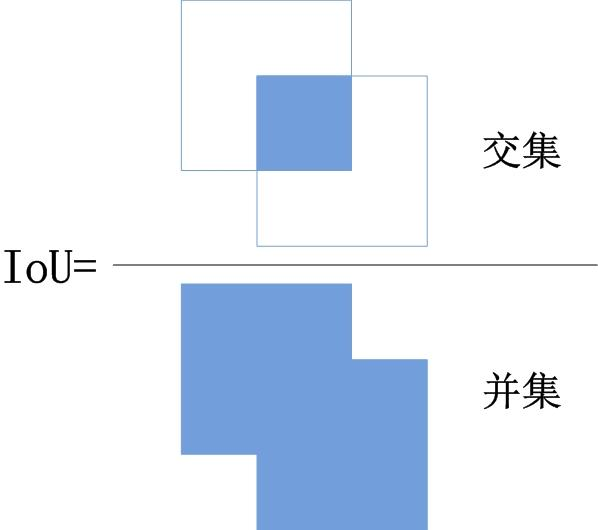
在分类任务中,可以对某一类别的预测结果和真实标签求IoU,例如对于二分类求正类的IoU如下:
也就是说,混淆矩阵中$i$行和$i$列的交集比上它们的并集。
平均交并比(mean IoU)就是对每一个类别求IoU,再求和求平均得到的值。
对于目标检测,IoU还有一个重要的应用,就是判断预测框与真实框的贴合程度,两部分重合面积越大,则IoU值越大。IoU是一个比较严格的评价指标,当两区域稍微有偏差时,IoU值也可能变得相当小,于是通常认为IoU大于$0.5$时就获得了一个比较不错的预测框。
参考文献
[1]https://zhuanlan.zhihu.com/p/111234566
[2]https://zhuanlan.zhihu.com/p/101566089
[3]https://blog.csdn.net/h1yupyp/article/details/80842172
[4]https://blog.csdn.net/lhxez6868/article/details/108150777
[5]https://zhuanlan.zhihu.com/p/371819054
[6]https://www.jianshu.com/p/22d947ffb71e
[7]https://zhuanlan.zhihu.com/p/372402161
[8]https://zhuanlan.zhihu.com/p/373658488
[9]https://zhuanlan.zhihu.com/p/373032887
[10]https://www.cnblogs.com/pythonfl/p/13705143.html
后记
首发于silencezheng.top。


