空洞卷积

前言

空洞卷积，Dilated Convolution，也可译为膨胀卷积或扩张卷积，可以使网络在不增加参数数量的情况下拥有更大的感受域。

提出

空洞卷积最初的提出是为了解决图像分割的问题，常见的图像分割算法通常使用池化层和卷积层来增加感受域，同时也缩小了特征图尺寸(resolution)，然后再利用上采样还原图像尺寸，特征图缩小再放大的过程造成了精度上的损失，因此需要一种操作可以在增加感受域的同时保持特征图的尺寸不变，从而代替下采样和上采样操作，在这种需求下，空洞卷积就诞生了。当然，跳跃连接（skip connection）也是另一种弥补信息损失的方法。

空洞卷积自2016在ICLR上被提出后，本身是用在图像分割领域，但立马被Deepmind拿来应用到语音(WaveNet)和NLP领域，它在物体检测也发挥了重要的作用。

原理

在常规卷积运算中，固定大小的滤波器在输入特征图上滑动，滤波器中的值与输入特征图中的相应值相乘以产生单个输出值。输出特征图中神经元的感受域被定义为滤波器可以“看到”的输入特征图中的区域。感受域的大小由滤波器的大小和卷积的步长决定。

相反，在膨胀卷积运算中，通过在滤波器值之间插入间隙来“扩张”滤波器。膨胀率(dilation rate) 决定了间隙的大小，它是一个可以调整的超参数。当膨胀率为 1 时，膨胀卷积简化为常规卷积。

膨胀率在不增加参数数量的情况下有效地增加了滤波器的感受域，因为滤波器的大小仍然相同，但值之间有间隙。这在需要更大感受域的情况下很有用，但增加滤波器的大小会导致参数数量和计算复杂性的增加。

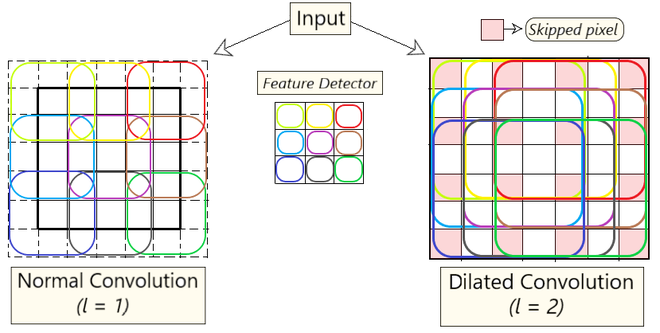
下图描述了正常卷积与扩张卷积之间的差异，附加参数$l$（膨胀因子）表示输入扩张了多少。换句话说，根据该参数的值，滤波器中会跳过$(l-1)$个像素。

膨胀卷积的公式可表示如下：

$$\left(F_{* l} k\right)(p)=\sum_{(s+l t=p)} F(s) k(t)$$

其中，$F(s)$为输入特征，$s$为各采样位置，$k(t)$表示卷积核$k$在$t$处的权重，${*l}$表示膨胀因子为$l$的膨胀卷积。

$(F_{* l} k)(p)$为在位置$p$处的输出。求和条件还需要再看下…

代码

在Pytorch中实现空洞卷积十分简单，只需要指定dilation参数即可。

class DilatedCNN(nn.Module):
  def __init__(self):
    super(DilatedCNN,self).__init__()
    self.convlayers = nn.Sequential(
      nn.Conv2d(in_channels = 3, out_channels = 6, kernel_size = 9, stride = 1, padding = 0, dilation=2),
      nn.ReLU(),
      nn.Conv2d(in_channels=6, out_channels=16, kernel_size = 3, stride = 1, padding= 0, dilation = 2),
      nn.ReLU(),
    )
    self.fclayers = nn.Sequential(
      nn.Linear(2304,120),
      nn.ReLU(),
      nn.Linear(120,84),
      nn.ReLU(),
      nn.Linear(84,10)
    )
  def forward(self,x):
    x = self.convlayers(x)
    x = x.view(-1,2304)
    x = self.fclayers(x)
    return x

可能产生的问题

1. 网格效应（The Gridding Effect）
2. Long-ranged information might be not relevant.

参考文献

[1] https://zhuanlan.zhihu.com/p/113285797
[2] https://www.geeksforgeeks.org/dilated-convolution/
[3] https://developer.orbbec.com.cn/v/blog_detail/892

后记

首发于 silencezheng.top，转载请注明出处。

赏

谢谢打赏哟！

支付宝

微信