并查集Disjoint Set Union

2024-10-28

字数统计: 2.1k字 | 阅读时长: 8分

前言

最近做笔试和刷题都遇到并查集（Disjoint Set Union, DSU）的题目了，学习一下。

并查集（Disjoint Set Union, DSU）

假设一个场景，$n$个人要么属于A帮派，要么属于B帮派，一个人属于某帮派的方式是直接或间接的给帮派老大打工，如何快速判断两人是否属于同一帮派呢？非常简单，看两人是否都给同一帮派老大打工就可以了。

由此引出一种数据结构：并查集。并查集用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

合并（Union）：把两个不相交的集合合并为一个集合。
查询（Find）：查询两个元素是否在同一个集合中。

并查集的一个应用前提是某一成员只能归属到至多一个分组之中。将集合的初始状态设置为所有成员都认为自己是帮派老大（分组根节点），然后通过成员关系（例如图上的连接关系）进行分组合并，最终会得到如下形式的分组结果，这些树状子结构的集合称为并查集。

并查集

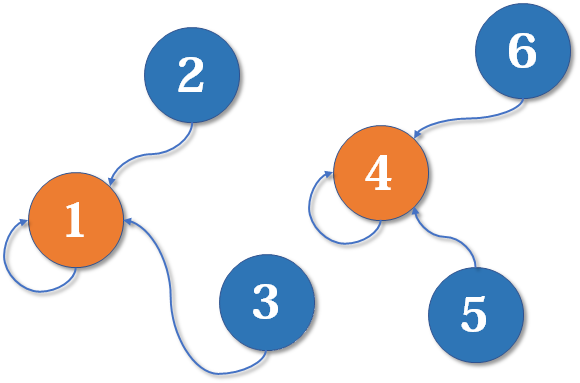
可以注意到每一个树状子结构存在唯一一个根节点，根节点自己也指向根节点，因此可以推出两种操作的实现：

合并（Union）：将B合并进A中，只需要将B的根节点指向A中的任意一个节点即可，但直接指向A的根节点可以最大程度的减少树高。
查询（Find）：查询某节点属于哪个集合，只需要递归的向上查找，直到找到自身指向自身的根节点。由此也可以得出结论，树高越低，查询效率越高。

最简实现

我们可以通过一个长度为$n$的数组来存储$n$个节点各自的父节点。初状态下各节点指向自身。操作的实现按照前面的分析进行，即“根合并到根”和”递归查询“。可以看到使用很少的代码量即可实现并查集结构。

// author: SilenceZheng66
public class SimpleDisjointSet {
    private int[] parent;

    // 初始化每个元素形成一个独立的集合
    public SimpleDisjointSet(int size) {
        parent = new int[size];
        for (int i = 0; i < size; i++) {
            parent[i] = i;  // 每个元素的父节点指向自己
        }
    }

    // 查找给定元素所属的集合的根节点
    public int find(int x) {
        if (parent[x] != x) {
            return find(parent[x]);  // 递归查找直到找到根节点
        }
        return x;
    }

    // 合并两个集合
    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            parent[rootX] = rootY;  // 将x所在的集合连接到y所在的集合，根合并到根
        }
    }

    // 测试方法
    public static void main(String[] args) {
        SimpleDisjointSet dsu = new SimpleDisjointSet(10);  // 创建一个大小为10的并查集

        // 执行一些合并操作
        dsu.union(1, 2);
        dsu.union(2, 3);
        dsu.union(4, 5);
        dsu.union(6, 7);
        dsu.union(7, 8);

        // 查询一些元素是否属于同一个集合
        System.out.println(dsu.find(1) == dsu.find(3));  // true
        System.out.println(dsu.find(1) == dsu.find(5));  // false
        System.out.println(dsu.find(6) == dsu.find(8));  // true
    }
}

路径压缩

在上面的实现中，其实已经做到了所谓的路径压缩，即尽可能减少树高，让帮派成员都直接给老大打工。

一种方式是从合并方法入手，另一种方式是从查询上实现路径压缩，这里给出从查询角度实现的代码。核心思想就是在每一次查询的递归过程中重构树，此时合并部分可以不用做压缩处理。

// author: SilenceZheng66
// 查找给定元素所属的集合的根节点
public int find(int x) {
    if (parent[x] == x) {
        return x;  // 找到根节点
    } else{
        parent[x] = find(parent[x]); // 递归过程中把非根节点都指向根节点
        return parent[x]; // 返回根节点
    }
}

// 合并两个集合
public void union(int x, int y) {
    parent[find(x)] = find(y); // 把x所在的集合合并到y所在的集合上
}

按秩合并

并查集容易陷入一个思维误区：应用路径压缩后，产生的树都是”菊花图🌼“，即只有两层的树，一个根节点和若干一级子节点。

可以证明实际情况并非如此：

1
2
3

// author: SilenceZheng66
dsu.union(1, 2); // 1 -> 2
dsu.union(2, 3); // 1 -> 2 -> 3

无论哪种路径压缩方法，在不执行查询的情况下，初始化并查集时仍会产生多层树。如下图所示，假设当前需要将节点$8$加入节点$7$的分组中，有两种情况。

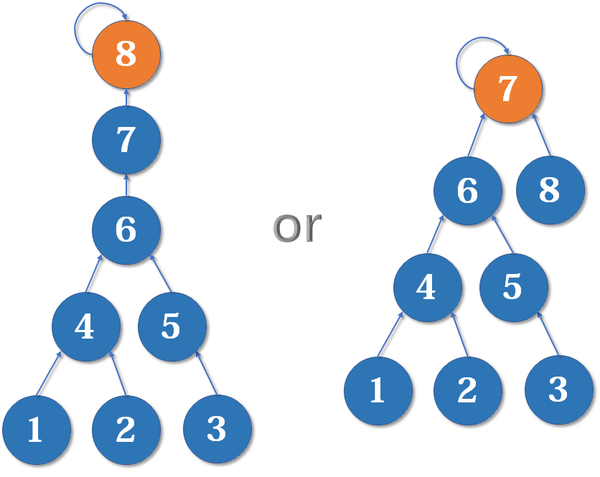
显然我们应该选择树高更低的合并方法，即把高度更低的树合并到更高的树上。

我们用一个数组$rank$记录每个根节点对应的树的深度（如果不是根节点，其rank相当于以它作为根节点的子树的深度）。一开始，把所有元素的rank（秩）设为1。合并时比较两个根节点，把rank较小者往较大者上合并。

// author: SilenceZheng66
public class DisjointSet {
    private int[] parent;
    private int[] rank;  // 用于记录每个节点所在树的高度（秩）

    // 初始化每个元素形成一个独立的集合
    public DisjointSet(int size) {
        parent = new int[size];
        rank = new int[size];
        for (int i = 0; i < size; i++) {
            parent[i] = i;  // 每个元素的父节点指向自己
            rank[i] = 0;    // 初始秩为0
        }
    }

    // 查找给定元素所属的集合的根节点，并进行路径压缩
    public int find(int x) {
        if (parent[x] != x) {
            // 路径压缩：将x直接指向其最终的根节点
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 合并两个集合，使用按秩合并
    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);

        if (rootX != rootY) {
            // 按秩合并
            if (rank[rootX] > rank[rootY]) {
                parent[rootY] = rootX;
            } else if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;
            } else {
                // 如果秩相同，则任意选择一个作为新的根节点，并增加该根节点的秩
                parent[rootY] = rootX;
                rank[rootX]++;
            }
        }
    }
}

路径压缩和按秩合并如果一起使用，时间复杂度接近$O(n)$，但是很可能会破坏rank的准确性。原因如下：

路径压缩的影响：
- 路径压缩在查找过程中将路径上的所有节点直接指向根节点，这会改变树的结构。
- 由于路径压缩改变了树的高度，但 rank 值并没有相应更新，因此 rank 可能不再准确反映树的实际高度。
按秩合并的假设：
- 按秩合并基于一个假设：rank 值反映了树的高度（或深度）。
- 如果路径压缩导致 rank 不再准确，那么按秩合并的效果可能会受到影响，因为合并操作依赖于 rank 来决定如何连接两棵树。

因此在同时使用的情况下，rank值事实上是树的高度上限。可以灵活选择如何使用按秩合并，考虑路径压缩的扰乱对整体效率的影响。

例题：Redundant Connection

如果两个顶点属于相同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间已经连通，因此当前的边导致环出现，为附加的边，将当前的边作为答案返回。

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        int[] parent = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            parent[i] = i;
        }
        for (int i = 0; i < n; i++) {
            int[] edge = edges[i];
            int node1 = edge[0], node2 = edge[1];
            if (find(parent, node1) != find(parent, node2)) {
                union(parent, node1, node2);
            } else {
                return edge;
            }
        }
        return new int[0];
    }

    public void union(int[] parent, int index1, int index2) {
        parent[find(parent, index1)] = find(parent, index2);
    }

    public int find(int[] parent, int index) {
        if (parent[index] != index) {
            parent[index] = find(parent, parent[index]);
        }
        return parent[index];
    }
}

参考文献

[1] https://zhuanlan.zhihu.com/p/93647900
[2] https://leetcode.cn/problems/redundant-connection/solutions/557616/rong-yu-lian-jie-by-leetcode-solution-pks2/?envType=daily-question&envId=2024-10-27

后记

首发于 silencezheng.top，转载请注明出处。