Trie字典树

2024-12-17

字数统计: 961字 | 阅读时长: 3分

前言

字典树，英文名 trie。顾名思义，就是一个像字典一样的树。

PS：某砍一刀大厂的手撕题目…当时直接不会换题了，现在回来还债。

引入

Trie

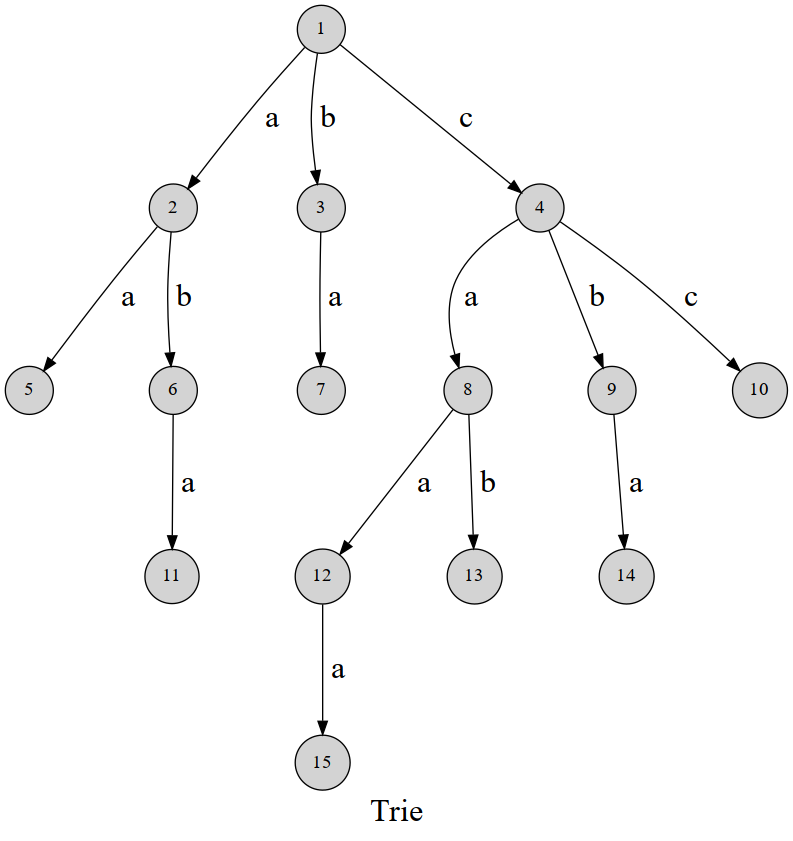
Trie如图所示，可以发现，这棵字典树用边来代表字母，而从根结点到树上某一结点的路径就代表了一个字符串。举个例子，$1\to4\to 8\to 12$ 表示的就是字符串 $caa$。

Trie 的结构非常好懂，我们用 $\delta(u,c)$ 表示结点 $u$ 的 $c$ 字符指向的下一个结点，或着说是结点 $u$ 代表的字符串后面添加一个字符 $c$ 形成的字符串的结点。（$c$ 的取值范围和字符集大小有关，不一定是 $0\sim 26$。）

有时需要标记插入进 trie 的是哪些字符串，每次插入完成时在这个字符串所代表的节点处打上标记即可。

实现

成员变量

int[][] tree = new int[10000][26];：
- 这是一个二维数组，模拟了字典树的节点。每个节点可以有最多26个子节点（对应于小写字母a-z）。tree[p][c] 表示从节点 p 出发，通过字符 c (‘a’ + c) 到达的下一个节点。
int cnt = 0;：
- 计数器，用来分配新的节点编号。每当插入一个新的分支时，cnt 增加，并为新节点分配一个唯一的ID。
boolean[] end = new boolean[10000];：
- 标记哪些节点是某个单词的结尾。end[p] == true 表示节点 p 是一个单词的结束位置。

方法

public void insert(String word)：
- 插入一个单词到字典树中。
  - 从根节点开始（p = 0），遍历单词中的每一个字符。
  - 对于每个字符，计算其相对于 ‘a’ 的偏移量 c，然后检查当前节点是否有对应的子节点。
  - 如果没有，则创建一个新的子节点，并更新 tree[p][c] 指向这个新节点。
  - 移动到下一个节点（p = tree[p][c]），继续处理下一个字符。
  - 最后，将到达的节点标记为单词的结束位置（end[p] = true）。
public boolean find(String word)：
- 查找一个单词是否存在于字典树中。
  - 从根节点开始（p = 0），遍历单词中的每一个字符。
  - 对于每个字符，计算其相对于 ‘a’ 的偏移量 c，并尝试移动到相应的子节点。
  - 如果在某一步无法找到对应的子节点，则返回 false，表示单词不存在。
  - 如果成功遍历完所有字符，最后检查到达的节点是否被标记为单词的结束位置（end[p]），如果是则返回 true，否则返回 false。

public class Trie {

    int[][] tree = new int[10000][26];
    int cnt = 0;
    boolean[] end = new boolean[10000];

    public void insert(String word) {
        int p = 0;
        char[] chars = word.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            int c = chars[i] - 'a';
            if (tree[p][c] == 0) {
                tree[p][c] = ++cnt;
            }
            p = tree[p][c];
        }
        end[p] = true;
    }

    public boolean find(String word) {
        int p = 0;
        char[] chars = word.toCharArray();
        for (int i = 0; i < chars.length; i++) {
            int c = chars[i] - 'a';
            if (tree[p][c] == 0) {
                return false;
            }
            p = tree[p][c];
        }
        return end[p];
    }
}

特点

高效性：插入和查找操作的时间复杂度都是 (O(L))，其中 (L) 是单词的长度。这是因为每次操作都只需要沿着路径逐层深入。
节省空间：相比于直接使用哈希表来存储单词，字典树能够更有效地利用公共前缀，从而减少内存占用。
支持前缀查询：除了完整单词的查找外，字典树还可以轻松扩展以支持前缀匹配或模糊查询等功能。

参考文献

[1] https://oi-wiki.org/string/trie/

后记

首发于 silencezheng.top，转载请注明出处。